Shor’un Algoritması ve RSA Kriptografisi’nin Düşüşü

Gelecek Bilimde Eylül 14, 2023

7 dakika okuma süresi

Yazan: Esat Canberk Özçelik

Düzenleyen: Ümit Sözbilir

Özet: Bu çalışmada, kuantum bilgisayarların gelişmesiyle tehdit edilen Rivest-Shamir-Adleman (RSA) kriptografisi ve olası alternatifleri üzerine incelemeler sunulmaktadır. RSA’yı güçlü kılan asıl faktör, büyük asal sayıların çarpımı kullanılarak elde edilen şifrelerin, bu şifrelenmiş veriye erişimi olmayan üçüncü şahısların kırabilmesi için tekrar o temel asal sayıları hesaplamaya kalktıklarında devasa zamanlara uzayan işlem sürecidir. Ancak Peter Shor’un 1994’te gösterdiği gibi, kuantum bilgisayarlar bunu klasik bilgisayarlardan çok daha hızlı yapabilir. Bu, RSA ve benzeri kriptografik şifrelemeleri alt üst etme potansiyeline sahiptir.
Shor Algoritması, kuantum süperpozisyonları aynı anda birçok çözümü ortaya çıkardığında beklenen yapıyı bulmak için Kuantum Fourier Dönüşümünü kullanır ve sonucunda işlem sürecinde eksponansiyel bir azalmaya yol açar. Bu araştırma, kuantum bilgisayarlar teknoloji ve algoritmalarının ilerlemesinin, yaygın olarak kullanılan mevcut kriptografik şifreleme yöntemleri, özellikle RSA için büyük bir tehdit oluşturduğunu göstermektedir. Makale, kriptografinin tarhini ve mantığını, günümüzdeki sistemlerin temel işleyiş prensipleri ile zaafiyetlerini anlatarak Shor algoritmasının rolüne ve ehemmiyetine değinmiştir.

Giriş

Şifrelerimiz, verilerimiz, banka hesapları, devlet verileri… hepsi çoğunlukla RSA (Rivest-Shamir-Adleman) şifreleme yöntemiyle korunuyor. Bu şifrenin kırılması en iyi bilgisayarlarla dahi yüzlerce, binlerce sene alıyor ve güçlü kılan özelliği de bu. Günümüz için gayet yeterli ve etkili bir yöntem olsa da gelişmekte olan kuantum teknolojileriyle büyük bir tehdit altında. Bu konuyu, önemini ve geleceğini daha iyi anlamamız için ilk olarak RSA şifrelemesinin ne olduğundan başlayalım.

Kriptografi

Kriptografi nedir? Saklı, gizli manasına gelen krypte (kript) ve yazı manasına gelen graphia (grafi) kelimelerinin birleşmesiyle meydana gelen kriptografi yani “saklı yazı” demektir [1]. Kriptografi yöntemlerinin amacını bilgiyi bir kişiden diğerine arada üçüncü bir kişinin bu bilgiye erişiminin önüne geçerek iletme yöntemi olarak özetleyebiliriz. Dikkat ederseniz bilgiye erişimini diyoruz çünkü mesaja erişebilir. Diyelim ki bir mektup gönderdik ve postacı bu mektubu açıp içindeki yazıyı okuyabilir, istenmeyen kişilerin eline geçebilir. Uygulanan şifrelemenin asıl amacı üçüncü bir şahıs gönderilen veriye erişse de içindeki bilgiye erişmesini önlemektir. Tarihe gidecek olursak bilinen en eski kriptografi yöntemlerinden birisi Sezar şifresidir. Farklı şekillerde uygulamaları yapılabilse de temelini şu şekilde arz edebiliriz:

Şifrelemek istediğimiz kelime “GELECEK”.

Alfabedeki her bir harf 1’den başlayarak numaralandırılır.

A	B	C	Ç	D	E	F	G	Ğ	H	I	İ	J	K	L
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M	N	O	Ö	P	R	S	Ş	T	U	Ü	V	Y	Z

16	17	18	19	20	21	22	23	24	25	26	27	28	29

Çizelge 1: Kelimelerin sayısal karşılıkları

“Gelecek” kelimesinin numaraları harf bazında bu hâli alır:

G	E	L	E	C	E	K
8	6	15	6	3	6	14

Çizelge 2: GELECEK kelimesinin Çizelge1’e göre sayısal karşılığı

Bir anahtar belirlenir. Örneğin $+2$ diyelim. Bu takdirde her bir harfin değeri $+2$ arttırılır. $-1$ deseydik de azalttırılırdı. Şifrelenmiş kelimemiz böyle gözüküyor:

H	G	N	G	D	G	M
8	6	15	6	3	6	14

Çizelge 3: GELECEK kelimesinin şifrelenmiş hâli

GELECEK kelimesini şifreledik ve HGNGDGM diye anlaşılmaz bir yazıya çevirdik. Karşı tarafın bunu okuması için anahtarımız olan $+2$ ‘yi bilmesi gerekir. Bu $+2$ ‘nin tersi olan $-2$ ‘yi kullanarak yani harf numarasına eklemek yerine şifrelemede uyguladığımızın tam tersi hareket ile çıkartarak kelimenin aslına erişebilir. Bu olayı matematiksel olarak değerlendirdiğimizde aslında bir fonksiyonla uğraştığımızı göreceğiz.

$F(x) = (x + k) \mod n$

$F$

= Şifre Fonksiyonu
$x$

= Asıl harfin numarası
$k$

= Kaydırma değeri
$n$

= Alfabedeki harf sayısı

Bu da anahtar fonksiyonumuz:

$F(y) = (y - k) \mod n$

$y$

= Saklı harfin numarası

Görüldüğü üzere üçüncü bir kişinin elindeki tek veri saklı harftir. Bu saklı harften şifreyi nasıl çözebilir, nasıl kırabilir? Çizelge 3’ü incelerseniz fark edeceksiniz ki aynı harfler hep aynı şekilde şifreleniyor. Sık çıkan harfleri analiz edip tahminler yürüterek şifreler kırılabilir. Bu yöntem döneminde başarılı olduysa da kâğıt kalemle oturup kırmak pek de zor değil zira deneyebileceğimiz farklı şifreler en fazla 28 tanedir. Bu yüzden çeşitli yaklaşım ve tekniklerle şifreleme yöntemleri geliştirilmiş ve kullanılmıştır, buna örnek olarak Vigenère Şifresi verilebilir¹. Yöntemlerden biri şifreyi kelime olarak seçmek. Mesela diyelim ki “Bilim” bizim şifremiz. Bu kelimeyi alfabe tablosunda numaralandırdığımızda $"2,9,12,9,13"$ olur. Tüm bir metni $+2$ , $-10$ gibi basit bir şekilde şifrelemek yerine bu anahtarla ilk harf $+2$ , ikincisi $+9...$ diye gider ve bir hayli çeşitlendirme yapılabilir. Tarih içinde de çeşitlendirilmeler yapılmış Vigenére şifresi gibi² farklı, gelişmiş teknikler ortaya atılmıştır.

Bu çeşitlemeleri çok iyi başaran bir cihaz ise 20. yüzyılın ilk yarısında Almanların kullandığı ENIGMA’dır. ENIGMA’nın özelliği bu şifreleme algoritmasını kağıt ve kalemle değil bir bilgisayarla yapıyor olması. Elektro-mekanik bir sistem yardımıyla Sezar şifrelemesinde çok daha karmaşık bir şifreleme ortaya koyar. Daktilonun bir tuşuna basınca rotorlar (döneçler) döner, içerideki kablolamalar değişir ve size her harf için başka bir sonuç verir. Sürekli değişen iç mekanizmasından ötürü bir düzen yakalamayı güç kılar. Ne kadar karmaşık olursa olsun her şifreleme gibi bu yöntemin de temeli bir matematiksel fonksiyona dayandırılabilir çünkü insanın en temel iç güdülerinden olan düzen arama devreye girer. Bu sistem, aynı harfleri aynı şifreler ile vermeyerek bunu güç kıldıysa da şöyle bir eksiği var ki şifrede asla kendisini vermiyor. Mesela E harfi alfabedeki herhangi bir harfe dönüşebilir, E dışında. Bu da şifrenin kırılması için takip edilebilir bir düzen yaratarak bir açıklık yaratıyor. Fakat Alman hava kuvvetlerinin kullandığı cihazlarda gelişmiş cihazlar kullanıldığı için bu sorun da yoktu. Yazışmalardaki olası benzerlikler gözetilerek Bombe adlı bilgisayar ile İngilizler şifreyi kırmayı başardı. Tabii her şifre kırılınca daha güçlüsünün yapılması gerekti. Binlerce yıldır bir yöntem geliştiriliyor ve güçsüz kaldığı her yeni gün daha güçlüleri yerini alıyor. Günümüz bilgisayarlarıyla ENIGMA şifrelerini kırmak mesele dahi değil. Şimdi ENIGMA’dan yaklaşık 40 yıl geleceğe atlayalım ve internet çağının başlarına gidelim.

RSA Kriptografisi

Whitfield Diffie ve Martin Hellman 1976 yılında yayımladıkları “Kriptografideki Yeni Yönler” adlı makalelerinde açık anahtarlı kriptografi konseptini öne sürüyorlar [3]. Bu da şu manaya geliyor: Şifreyi kırmak için iki adet anahtara ihtiyaç var birisi gizli, alıcı ve göndericide durur ve asla paylaşılmaz, diğeri ise açık anahtar ki bu da mesaj ile beraber gönderilir. Sadece bu anahtarla şifre açılamayacağı için zaafiyet yaratmaz. Bu anahtarlar ise büyük asal sayılardır. Fakat bu fikri yürülüğe koymak için tek yönlü bir fonksiyonun türerilmesi gerekiyordu. Bunu ise üç MIT (Massachusetts Institute of Technology) öğrencisi başardı.

RSA (Rivest–Shamir–Adleman) kriptografi sistemi adını üç mucidinin soy isimlerinin baş harflerinden alıyor. Ron Rivest, Adi Shamir ve Leonard Adleman. 1977 yılında yayınladıkları “Dijital İmzalar ve Açık Anahtar Kripto-Sistemleri için Bir Metod” [4] adlı makalelerinde Diffie ve Hellman’ın ortaya attığı problemi çözüp kriptografide yeni bir yön açtılar. Bu algoritma, basit ve etkili olması sebebiyle, çıkışından günümüze kadar önemini ve kullanışını koruyor.

(soldan sağa) Ronald Rivest, Adi Shamir, ve Leonard Adleman (2003) [5]

RSA’nın temelini, asal sayılar oluşturur. İlk olarak, iki adet büyük asal sayı seçilir³⁴ ve genellikle bu sayılar matematiksel olarak ifade edilmesi için $p$ ve $q$ şeklinde adlandırılır. Bu asal sayıların seçimi ve büyüklüğü, algoritmanın güvenliğini doğrudan etkiler. Daha sonra, bu iki sayının çarpımı alınır, bu çarpıma ise $n$ denir ve sonunda böyle bir denklem elde edilir: $n = p \times q$ .

Bu noktada, aralarında asal sayıları bulmak için Euler’in Totient Fonksiyonu⁵ olarak adlandırılan bir değeri hesaplamamız gerekiyor. Bu değer genellikle $\varphi(n)$ ile gösterilir ve $\varphi(n) = (p-1) \times (q-1)$ şeklinde hesaplanır. Bir sonraki adım, $1$ ile $\varphi(n)$ arasında bir tam sayı $e$ seçmektir böylece $e$ ‘nin $\varphi(n)$ ile aralarında asal olması sağlanır. $e$ , kamuya açık anahtarda kullanılır ve genellikle küçük ve standart değerler (örneğin, $3$ veya $65.537$ ) kullanılır. Son adımda, $1$ ile $\varphi(n)$ arasında bir $d$ değeri bulunur, böylece $(d \times e) \bmod \varphi(n) = 1$ eşitliği sağlanır. $d$ , özel anahtarda kullanılır. Bu sürecin sonunda, kamuya açık anahtar $(e, n)$ ve özel anahtar $(d, n)$ olarak belirlenmiş olur.

RSA şifrelemesi için, bir mesaj ( $M$ ) alınır ve şifreli bir metin ( $C$ ) oluşturulur:
$C = M^e \bmod n$

Deşifreleme işlemi, bu şifreli metni orijinal mesaja dönüştürmek için özel anahtarı kullanır:
$M = C^d \bmod n$

Sorun

Bahsettiğimiz üzere bu sistem büyük ve hesaplanması zor sayıları kullandığı için gayet sağlam ve işlevli bir araç olmuştur fakat hatırlamakta fayda var ki hesaplanması klasik bilgisayarlar için gereketirdiği işlem gücünden ötürü bir hayli güçtür ve yüzyıllara varan ve hatta aşan süreler gerektirir. Burada kuantum bilgisayarlar devreye giriyor. Kuantum bilgisayarların tarihsel gelişimine baktığımızda, 1980’lerin başlarında Richard Feynman’ın “Bilgisayar ile Fizik Simülasyonları”[6] makalesinde kuantum mekaniklerini simüle etmek için kuantum sistemlerini kullanma fikrinin ilk ortaya atıldığı kağıtlardandır. Bir süre boyunca bu fikirler teoride kalsa da 1990’lı yıllara gelindiğinde kuantum algoritmaları ve kuantum hesaplama alanındaki çalışmalar hız kazanıyor.

1994 yılında, MIT’den Peter Shor, kuantum bilgisayarlar üzerinde çalışmak üzere tasarlanmış olan Shor Algoritması’nı yayımladı [4]. Shor Algoritması, klasik bilgisayarlarla polinomsal zamanda çözülemeyen bir problem olan büyük sayıları asal çarpanlarına ayırmada devrim niteliğinde bir hız sunuyordu. RSA şifrelemesinin temelini oluşturan bu zorlukğun kuantum bilgisayarlarla aşılabileceği anlaşılınca, kriptografi alanında büyük bir endişe yarattı.

Shor Algoritması’nın işleyişine bakacak olursak; bu algoritma, kuantum mekaniklerinin süperpozisyon ve ölçüm ilkelerini kullanır. Algoritma, öncelikle bir kuantum süperpozisyonu oluşturarak aynı anda çok sayıda çözümün üzerinde çalışır. Bu süreç, Kuantum Fourier Dönüşümü adı verilen bir teknikle yapılır ve periyodik bir yapı bulmaya yardımcı olur.

Shor Algoritması’nın temel adımları şunlardır:

Rastgele bir sayı seçilir ve bunun, asal çarpanlara ayrılacak olan sayı ile aralarında asal olup olmadığı kontrol edilir.
Eğer asalsa bu sayıyı kullanarak bir süperpozisyon oluşturulur.
Kuantum Fourier dönüşümü uygulanarak periyodik bir yapı aranır.
Bulunan periyodik yapı, asal çarpanları bulmak için kullanılır.

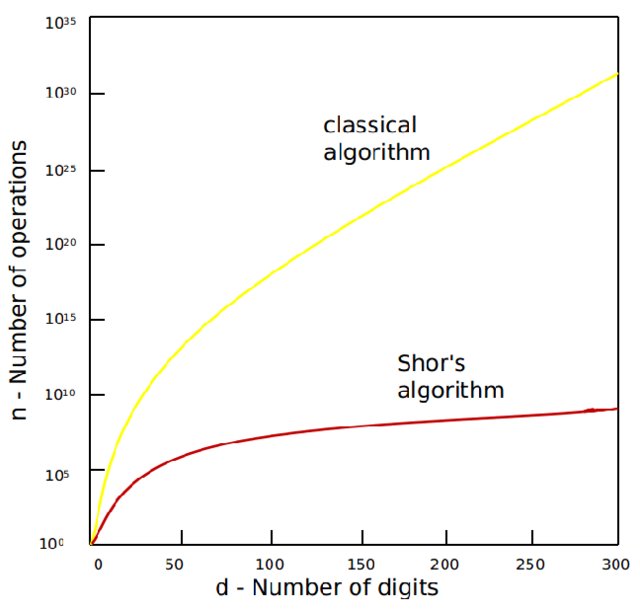
Basamak sayısı ile gereken operasyonların tablosu [7]

Bu süreç klasik algoritmaların yapabileceğinden eksponansiyel bir farkla daha hızlıdır ve RSA gibi kriptografik şifrelemeleri tehdit eder. Shor Algoritması’nın varlığı, kuantum bilgisayarların gelişimi ile birlikte kriptografi alanında yeni şifreleme yöntemlerinin geliştirilmesi gerektiğini göstermektedir.

Günümüzde kuantum bilgisayarları kübit (qubit)⁶ bakımından Shor’un algoritmasını, RSA şifrelemesini kıracak nitelikte çalıştırmaya yeterli olmadığı için klasik algoritmalar gayet güvenilir bir şekilde işlevini yerine getiriyor fakat teknoloji ve araştırmaların yine günümüzdeki ivmelenmesine bakacak olursak klasik kriptografi ilerleyen yıllarda devlet, ordu, banka gibi kimi ehemmiyet teşkil eden yerlerde yerini kuantum kriptografiye bırakacak gibi gözüküyor.

Sonuçları

RSA kriptografisi günümüzde hemen hemen her yerde şifrelemenin temelini oluşturuyor ve yaygın olarak kullanılıyor. Alternatifleri ise RSA’nın bir varyasyonundan yola çıkıyor. Bankalar, devletler, askeriye, istihbarat, internet siteleri, oyunlar… kısacası bu, bilginin depolandığı her yeri ilgilendiren bir durum. Bu teknolojide kim ilk zafer kazanıp tam manasıyla algoritmayı işleme sokarsa ya da hatta daha gelişmiş algoritmalar ile bunu uygularsa iyimser bir bakış açısıyla kendisini olası tehditlere karşı koruyabilir.

¹ Detaylı okuma ic¸in bu makale incelenebilir: (Al-Amin Mohammed Aliyu and Abdulrahman Olaniyan. “Vigenere Cipher: Trends, Review and Possible Modifications”. In: International Journal of Computer Applications 135.11 [Feb. 2016], p. 46. ISSN: 0975-8887)

² Giovan Battista Bellaso tarafından 1553 yılında La cifra del kitabında açıklanan bir şifreleme türü. Örneğini verdiğimiz şifre olarak kelime metodunu kullanır ve tekrar eden harflerin bir nebze önüne geçer.

³ Whitfield Diffie and Martin E. Hellman. “New Directions in Cryptography”. In: IEEE Transactions on Information Theory IT-22.6 (Nov. 1976).

⁴ Bu sayıların büyük seçilmesinin sebebi, pratikte kırmak için gereken süreyi uzatmaktır. Bu sayılar yüzlerce ondalık basamak değerinde olabilir. Klasik bilgisayarlarda en küçük veri birimi olarak “bit” olarak adlandırılan 0 ve 1 kullanılır. Bir veri 0 yahut 1 olabilir. Kuantum sistemlerde ise süperpozisyon adı verilen daha karmaşık haller de mevzubahis olduğundan ötürü “kuantum bit” söyleminden kısaltılan “kübit” kelimesi kullanılır.

⁵ Euler’in Totient Fonksiyonu $\varphi (n)$ , bir sayının kendisinden küçük olan ve onunla aralarında asal olan sayıları hesaplamakta kullanılan bir fonksiyondur. Örneğin, $p=5$ , $q=3$ ; $\varphi(15) = (5-1) \times (3-1)=8$ . Bunun manası, $15$ ‘den küçük olan ve $15$ ile aralarında asal olan $8$ sayı olduğunu gösterir. $1, 2, 4, 7, 8, 11, 13, 14$ .

⁶ Klasik bilgisayarlarda en küçük veri birimi olarak “bit” olarak adlandırılan 0 ve 1 kullanılır. Bir veri 0 yahut 1 olabilir. Kuantum sistemlerde ise süperpozisyon adı verilen daha karmaşık haller de mevzubahis olduğundan ötürü “kuantum bit” söyleminden kısaltılan “kübit” kelimesi kullanılır.

Referanslar

Anahtar Kelimeler