Sonsuzluk Çıkmazı

Yazan: Kübra Nur Canbay

Düzenleyen: Ümit Sözbilir

Özet: Sonsuzluk anlaşılması hem zor hem de kolay bir kavramdır. Düşünebildiğimiz kavramlar aslında sonlu kavramları içerir. Günlük hayattaki sonsuzluk kavramından matematiksel sonsuzluk kavramına doğru yol aldığımızda durum biraz daha karmaşık hâle gelir. Ancak matematikteki sonsuzluk bir sıfat olarak ele alınmalıdır.

Giriş 

Sonsuzluk kavramı anlaşılması hem kolay hem de çok zor bir kavramdır. Günlük yaşantımızda sonsuzluk kavramı bazı zihinler için çok büyük, çokluk gibi anlamlara gelirken sonsuzluk aslında düşüncenin dahi ulaşamadığı yer olmalıdır. Düşünebildiğimiz bir şey aynı zamanda sonlu bir şeydir. Sonsuzluk kavramı ancak sonlu bir kavramın zıttı olarak değerlendirilebilir. Beynimiz bir şeyi zıttı ile mukayese etmeye meyillidir. Konumuz matematiğe gelince ise sonsuz ya da sonsuzluk kavramı çok uzun yıllar boyunca temkinli yaklaşılan, çok fazla içine girilmek istenmeyen ancak yok sayılması da pek mümkün olmayan bir yerdedir. Bu iki kavram matematiksel açıdan sıfat olarak algınlanmalıdır. 

Zeno’nun Çıkmazı: Aşil ve Kaplumbağa

Sonsuzluk çıkmazlarının en eski ve en ünlülerinin arasında eski Yunan filozofu Zeno’nun çıkmazları yer alır. Bu çıkmazlar günümüze kadar ulaşmış, uzun yıllar boyunca dönemlerin ünlü matematikçileri, fizikçileri tarafından tartışılmış ve üzerine düşünülmüştür. Zeno en bilindik çıkmazlarının birinde Aşil¹ ve kaplumbağayı yarıştırır. Aşil 1m/s hızla koşarken kaplumbağanın 0,1 m/s hızla ilerlediğini varsayalım. Kaplumbağa çok yavaş olduğu için yarışa Aşil’in 0,9 metre önünde başlar. Aşil’in kaplumbağayı yakalayabilmesi için kaplumbağanın yarışa başladığı noktaya ulaşması gerekir. 1 sn. sonra Aşil’in kaplumbağayı başladığı yerden 0,1 metre uzaklıkta yakalaması gerekir. Ancak Aşil’in harcadığı bu süre içerisinde kaplumbağa bir miktar daha ilerlemiş olur. Bu durumda Aşil’in yeni noktaya ulaşması gerekir. Bu süre içerisinde kaplumbağa yine bir miktar yol kateder. Aşil’in, kaplumbağanın olduğu noktaya her varışında aslında kaplumbağa bir miktar daha ilerlemiş olur. Aşil’in her seferinde yeniden koşması gereken bir yolu vardır ve bu sonsuza kadar bu şekilde devam eder. Bu yarışı matematiksel olarak ifade etmek gerekirse Aşil’in koşusu 0,9 m, 0,99 m, 0,999 m, …, 1 m noktalarını içeridir. Bu koşu içersinde sonsuz tane uzaklık değeri bulundurur. “Böyle bir diziyi matematiksel olarak ifade edebilir miyiz?” sorusu matematiksel bir soruna yol açar. Bu ve benzeri çıkmazların ortak özelliği sonlu bir sürede sonsuza giden bir devinimin olmamasıdır. İlk sorundan çıkmak çok kolay olmasa da ünlü matematikçi Cantor’un öncülüğünü yaptığı sonsuz seriler çalışması belli ölçüde açığa kavuşturmuş ve matematiksel olarak kabul edilebilir bir yere gelmiştir. Bu süre içinde çözüm arayışları başka bir soruna sebep olmuş ve matematikçileri geometriye doğru bir yolcuğa çıkarmıştır.

Doğru Parçası Çıkmazı

Tarihi Zeno’nun çıkmazları kadar eski olan doğru parçası çıkmazıyla devam edelim. Nokta nedir? Noktanın bir tanımını vermek mümkün müdür? Çok standart bir tanımlamadan elbette bahsedebiliriz, boyutu olmayan bir iz, belirti nokta olarak kabul edilebilir. Doğru parçasını tanımlarken ise sonsuz adet noktadan oluşan başlangıç ve sonu olan bir doğru diyebiliriz. Peki boyutu olmayan bu küçük iz yani nokta nasıl olur da şekli ve boyutu olan bir doğru oluşturabilir? Eğer oluşturur dersek noktanın az da olsa bir boyutunun olduğunu kabul etmemiz gerekir. Ancak bu kez nokta tanımında bir çelişki meydana gelir. O güne kadar bilinen tek geometri sistemi olan Öklid geometrisi bu çelişkiye cevap verecek yetkinliğe sahip değildir. Beş belitten² oluşan Öklid geometrisinin beşinci beliti, paralellik beliti olarak da bilinen, “Paralel düz doğrular aynı düzlemde bulunan ve her iki yönde de birbirleriyle kesişmeyen doğrulardır.”  ifadesidir. Eş değerlik gereği, ilk dört belitin ve bu belitlerden herhangi birinin beşinci belite karşılık gelmeli ve beşinci belit de ilk dört belitin hepsini karşılamalıdır. İlk dört belit şu şekildedir [2]:

1. Eğer bir düz doğru paralel olanlardan birini kesiyorsa diğerini de keser.
2. Aynı düz doğruya paralel olan düz doğrular birbirine paraleldir.
3. Birbirini kesen iki düz doğru aynı doğruya paralel olamaz.
4. Düzlemde bir L doğrusu ve bu doğru üzerinde olmayan bir P noktası verilsin. Bu durumda, P noktasından geçen ve L doğrusuna paralel olan bir ve ancak bir doğru vardır.

Beşinci belitle ilgili şüpheler giderilmeye çalışılmış ancak bu belitin diğerlerinden türetilemeyeceği sonucuna ulaşılmıştır. Bu sorun Öklid dışı geometrilerin oluşmasına neden olmuştur. 

Cusa’lı Nicholas’ın Sonsuz Küçük Argümanı

Öklid dışı geometrilere açılan kapıların en önemlilerinden birisi Cusa’lı Nicholas³ tarafından ortaya konan sonsuz küçüklerin kullanıldığı bir argümandır. Nicholas sonsuz büyük ve sonsuz küçüğü çalışırken daireyi kullandı. Aslında buradaki amacı, dini öğretisinde kişinin gerçeğe yaklaşabileceğini ancak asla tam olarak ulaşamayacağını göstermekti. Ancak dini öğretisi için araç olarak matematiği kullanması sonsuzluk kavramına da büyük katkılar sağladı. Çalışmalarının çoğunda dairenin karesini alma ve dairenin çevresini ölçme problemini ele aldı. Nicholas’ın görüşünü şöyle ifade edebiliriz: Bir dairenin çevresi ve alanı arasındaki ilişkiyi bulmaya çalışalım. , bir dairenin yarıçapı olmak üzere  olsun. Dairenin çevresi sonsuz sayıda doğru parçalarından oluşsun. Bu durumda daire, yüksekliği 1 olan sonsuz küçük üçgenden oluşmaktadır. Bu üçgenlerin alanın toplamı dairenin alanın toplamına eşit olacaktır. Üçgenin tabanlarının toplamı ise dairenin çevresine eşittir ancak sonsuz küçük tabanı olan bir üçgen oldukça zor anlaşılır bir kavramdır. Üçgenin tabanı 0 olursa sonuç zaten 0’dır. Peki üçgenin tabanı 0’dan büyükse ne kadar küçük olursa olsun sonsuz terimi toplarsak sonsuz büyüklük elde ederiz. Her iki durumda da çemberin sonlu çevresine, sonsuz tane özdeş parçanın toplamından ulaşamayız. Matematiksel açıdan karşımıza yeni bir çelişki çıktı.

Kepler’in Şarap Fıçısı

Nicholas’ın açtığı yoldan Kepler⁴ yürümeye devam etti. Kepler ikinci evliliği sırasında yaşadığı bir olay matematiğe büyük bir katkı sağladı. Düğünü için şarap fıçısı satın alan Kepler, satıcının hacim ölçme yöntemine sinirlendi. En iyi şarap fıçısının oranlarını bulmak için, katı cisimlerin alan ve hacim hesapları üzerine yapılmış çalışmaları incelemeye başladı. Kepler’in yaklaşımı, belirli bir katıyı uygun boyut ve şekilde sonsuz sayıdaki sonsuz küçük parçalara ayırmaktı. Kepler fıçıyı ince katmanlardan oluşan bir yığın olarak kabul etti. Yapması gereken şey tüm katmanların hacmini bulmaktı. Sonsuz küçük kavramını kabul ettiği için yaptığı hesap doğru kabul edilebilirdi. Nova Stereometria Doliorum Vinariorum⁵ adlı eserinde yaptığı çalışmalarını anlattı. [4] 

Newton ve Leibniz: Sonsuz Küçüklerin Analize Yolcuğu

Sonsuz küçüklerin bir sonraki akıl yürütücüleri Newton⁶ ve Leibniz⁷ olmuştur. Aslında her ikisi de sonsuz küçük kavramından kaçınmayı ve uzak durmayı tercih ediyorlardı. Ancak Robinson⁸ tarafından tekrar gündeme getirilen sonsuz küçükler Leibniz’i bu alana itmiş oldu. Geometriden sonra analize doğru yolcuğuna devam eden sonsuz küçükler bu kez anlık hız problemleriyle bağlantı kurmaya yönlendirildi. Sorulardan birisi şuydu: Düşen bir cismin  anındaki hızını nasıl hesaplayabiliriz?  Sonlu bir zaman içerisindeki ortalama hızı, yolu zamana bölerek bulabiliyoruz. Peki anlık hız için de aynı formülü kullanmak mümkün müdür? İşte Newton ve Leibniz bu alandaki çalışmalarıyla sonsuz küçükler hesabını biçimlendirdi diyebiliriz. , yol; , mesafe olmak üzere; , zamandaki sonsuz küçük artış; , bu zamandaki mesafe artışını temsil etsin. Bulmak istediğimiz sonlu oran ise  . Bu formülde  almamız ifadeyi tanımsız yapar.  ise bölünemez. Bu durumda sonsuz küçük terimini atarak bir sonuca ulaşabiliriz. Anlık hız ise tam olarak hesaplanamamış olur. Berkeley⁹, bu biçimlendirmeye karşı çıkmıştır. Çünkü ihmal edilen şey aşırı küçük olsa bile ihmal edilmesi ancak yaklaşık sonucu bulmaya fırsat verebilir. Berkeley’in, bu yönteme olan eleştirisi The Analyst’deortaya çıktı. Berkeley’in eleştirisine bir itiraz sunmak çok mümkün olmasa da matematikçiler uzun süre başarıyla sonsuz küçükleri bu şekilde kullanmaya devam etti. [6] 

Weistrass ve Cauchy: Limite Doğru

On dokuzuncu yüzyıla geldiğimizde tüm bu gelişmeler Weistrass¹⁰ ve Cauchy¹¹ tarafında toparlanıp düzene koyuldu. Hızı bir oran olarak hesaplamak yerine bir limit olarak tanımlamayı önerdiler. Hızın limit tanımı: Her  pozitif sayısı için ’nin mutlak değerinin diğer bir  pozitif sayısından küçük olduğu her değerde, ’nin mutlak değeri ’dan küçük oluyorsa hız ’dir. [2] Diyelim ki  değişken bir zaman artışını,  ise bu zamana karşılık gelen değişken mesafe artışını temsil etsin. Bu durumda ’nin değerine istediğimiz kadar yaklaşabiliriz. Limit ile yapılan bu yaklaşım Berkeley’in ileri sürdüğü eleştirilerden de kurtarmış oldu. Tabii ki bu durum limit gibi anlaşılması güç bir kavrama bağımlılık oluşturmuştu. Hız, ve  gibi iki yeni nicelikle tanımlanmış oldu. Analizdeki bu gelişme limit ve epsilon-delta () kavramını yeniden yapılandırılmış, reel sayıları indirgemeye doğru gitmiştir. Sonsuz küçük reel sayılar kavramı matematikte yer bulmaya çalışmıştır. Ancak Arşimet’in teoremi reel sayılarda sonsuz küçük olamayacağını ortaya koymuştur. Teorem bize şöyle der: “Sıfırdan büyük olan her doğal sayıdan küçük bir eleman olamaz.” [8] Bu gelişmeden sonra Robinson ile sonsuz küçükler kavramı standart dışı analize taşınmıştır. Robinson’un sistemine göre anlık hızda ölçülebilir olan reel kısımdır, diğer kısmı ise kabul ederiz. Yani anlık hız ölçülemez, yaklaşık değeri reel sayılara bağlı olarak hesaplanır.

Cantor: Sonsuz Büyükler

Geometrinin devrimine benzer bir devrim soyut kümeler kuramında da yaşanamıştır. Cantor¹², sonsuz kümeler tanımını şöyle verebiliriz: “Özalt kümesine eşit güçlü olan kümelere sonsuz kümeler denir.” Buradaki eşit güçlü kavramı, kümenin birebir ve örtenliği sağlamasıdır. Bunu da aç gerekirse iki kümenin elemanlarını açıkta eleman kalmayacak şekilde birebir eşleyebiliyorsak bu iki küme eş değerdir deriz. Cantor’a göre tüm çift sayılar kümesi doğal sayılarla eşlenebilir. Benzer şekilde bu kümeler tam kare sayılar kümesiyle de eşlenebilir. Ancak bütün sonsuz kümelerin eleman sayısının aynı olmaması en az iki türde sonsuzluğu ortaya çıkarır. İşte Cantor’un kuramındaki ilk büyük keşfi de bu olmuştur. İlk olarak doğal sayıların sonsuzluğu ile başlayalım. Yani doğal sayıların kardinaletisi ’dır, buna alef sıfır da denir. Kardinaletisi alef sıfır olan kümeler sayılabilir kümeler olarak ifade edilir. İkinci küme olarak bir doğru parçası tarafından temsil edilen sonsuzluğu seçelim,  aralığı gibi. Bu kümelerin kardinalitesi ise  ile gösterilir. , sürekli bütün anlamına gelen “continuum” kelimesinden gelir. Herhangi bir uzunluktaki doğru parçasının, düzlemdeki bir üçgenin veya uzaydaki bir küpün kardinalitesi ’dir. Matematiksel olarak ifade edersek doğal sayılar kümesi olmak  üzere alt kümesi sayısı olan , sürekli bütüne yani keyfi bir doğru parçası olan ’ye eşdeğerdir. olur. Peki  ile  arasında sonsuz bir küme var mıdır? Bu soru Cantor’un aklına gelmiştir ama böyle bir küme bulamamıştır. İlerleyen yıllarda meşhur eksiklik teoremlerinin sahibi olan Kurt Gödel tarafından ’dan büyükk ancak ’den küçük bir sonsuz kardinalin ispatlanamayacağı sonucuna ulaşılmıştır.

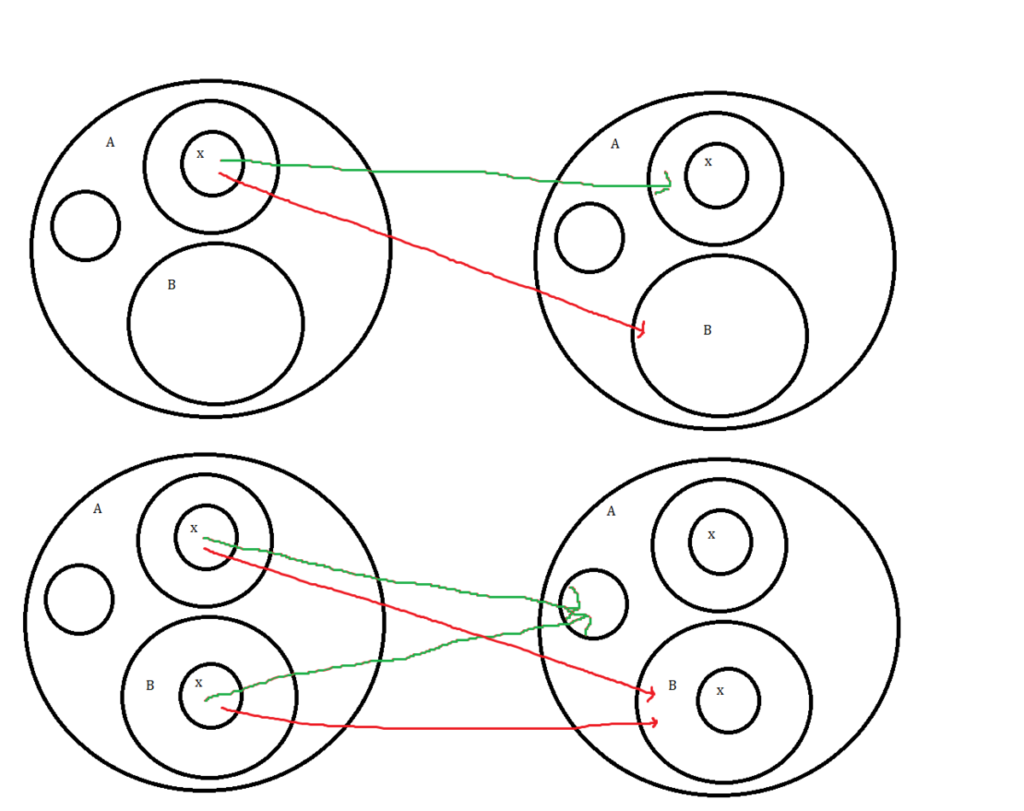
Dönemin ünlü matematikçilerini etkisi altına alan sonsuzluk kavramı, ulaşılan çözümler sonucunda yeni soruları, sorunları beraberinde getirmiştir.

Hilbert’in Sonsuzluk Oteli

Cantor’un teorisine bir de Hilbert’in Sonsuzluk Oteli örneğiyle bakalım. Bu örnek, teorinin dünyaya nasıl uygulanabileceğini göstererek konuyu zihnimizde biraz somutlaştırabilir. Hilbert’in Sonsuzluk Oteli, her katında bir oda bulunan, sonsuz kattan oluşan ve sonsuz sayıda müşterinin olduğu bir yerdir. Sonsuz katlı bu otel, sonsuz müşteriye sahip olduğu için tamamen doludur. Peki, bir müşteri bu otele kalmak için gelsin. Sizce bu müşteriye bir oda bulmak mümkün müdür? Müşteriye oda ayarlayacak isim Cantor ise cevabımız evet. Çünkü Cantor’un teorisine göre ’dır. Şimdi otele geri dönelim, otelde kalan her müşteri bir üst kata taşınırsa ilk kata yeni gelen müşteri yerleşebilir. Benzer şekilde bu işlemi sonsuz kere tekrarlamak mümkündür. 

Sonsuzluğun Sonucu 

Matematikte kullanılan sonsuzluk bir sıfat olarak kullandığı için bir çelişki oluşturmaz. Mesela iki sayısının fiziki bir karşılığı dünyada yoktur ancak iki arabanın fiziksel karşılığı mevcuttur. Burada iki tek başına potansiyel bir varlığa sahip iken sıfat olduğu zaman fiziksel bir varlığa sahip olur. Sayılar potansiyel bir sonsuzluğa sahiptir dersek herhangi bir çelişki oluşturmayız. Bir başka açıdan bakarsak, doğal sayıları düşünelim. Doğal sayılar sonsuz elemanlı bir kümedir. En küçük doğal sayıyı sorduğumuzda 0 cevabını alabiliriz. Peki biz en büyük doğal sayının hangi sayı olduğunu cevaplayabilir miyiz? Burada, sonsuzdan büyük bir mutlak sonsuz daha vardır dersek tutarlı olmayan bir şey söylememiş oluruz. Mutlak en büyük sonsuz ise ondan daha büyük sonsuz yoktur demek sonsuzluğun tanımı ile çelişir. Matematiksel olarak bundan kurtulmanın yolu bir kümenin içinde başka bir kümenin olmadığını kabul etmektir. Buradan geriye kalan sonsuzluk kavramı felsefeciler arasında tartışılabilir, matematikteki sonsuz kavramı sıfat olarak kabul edilir ve tek başına sonsuzluk fiziki olarak bir karşılık barındırmaz.

¹ Yun. Ἀχιλλεύς. Akhilleus. Annesi tanrı, babası ölümlü bir kral olan yarı tanrıdır. Truva Savaşı’nın Yunan kahramanlarının başında gelir ve Homeros’un İlyada adlı mitolojik eserinde Yunanlıların en büyük savaşçısı olan başkarakterdir. 

² İng. axiom

³ Alman Nikolaus Von Cusa. Hristiyan bir bilim insanı. Teoloji, matematik, felsefe alanlarında önemli çalışmalarda bulunmuştur.

⁴ Johannes Kepler. Alman gök bilimci, matematikçi. Gezegen hareketi yasası ile tanınır.

⁵ Bir Şarap Fıçısının Hacmi. 

⁶ Sir Isaac Newton. İngiliz matematikçi, fizikçi. Üç hareket yasası ve evrensel kütle çekimi yasasını formülüze etmiştir.

⁷ Gottfried Wilmhelm. Leibniz. Alman matematikçi, filozof.

⁸ Abraham Robinson. Polonyalı matematikçi. Standart dışı analizin önemli temsilcisi.

⁹ George Berkeley. İngiliz piskopos, felsefeci. The Analyst adlı eseriyle matematiğe de büyük katkıları olmuştur.

¹⁰ Karl Weierstrass. Alman matematikçi. Analizin en önemli temsilcilerinden. 

¹¹ Augustin-Louis Cauchy. Fransız matematikçi. Kompleks analizin önemli temsilcisi.

¹² Georg Cantor. Alman matematikçi. Kümeler kuramının kurucusu.